CARS: Progress Chart

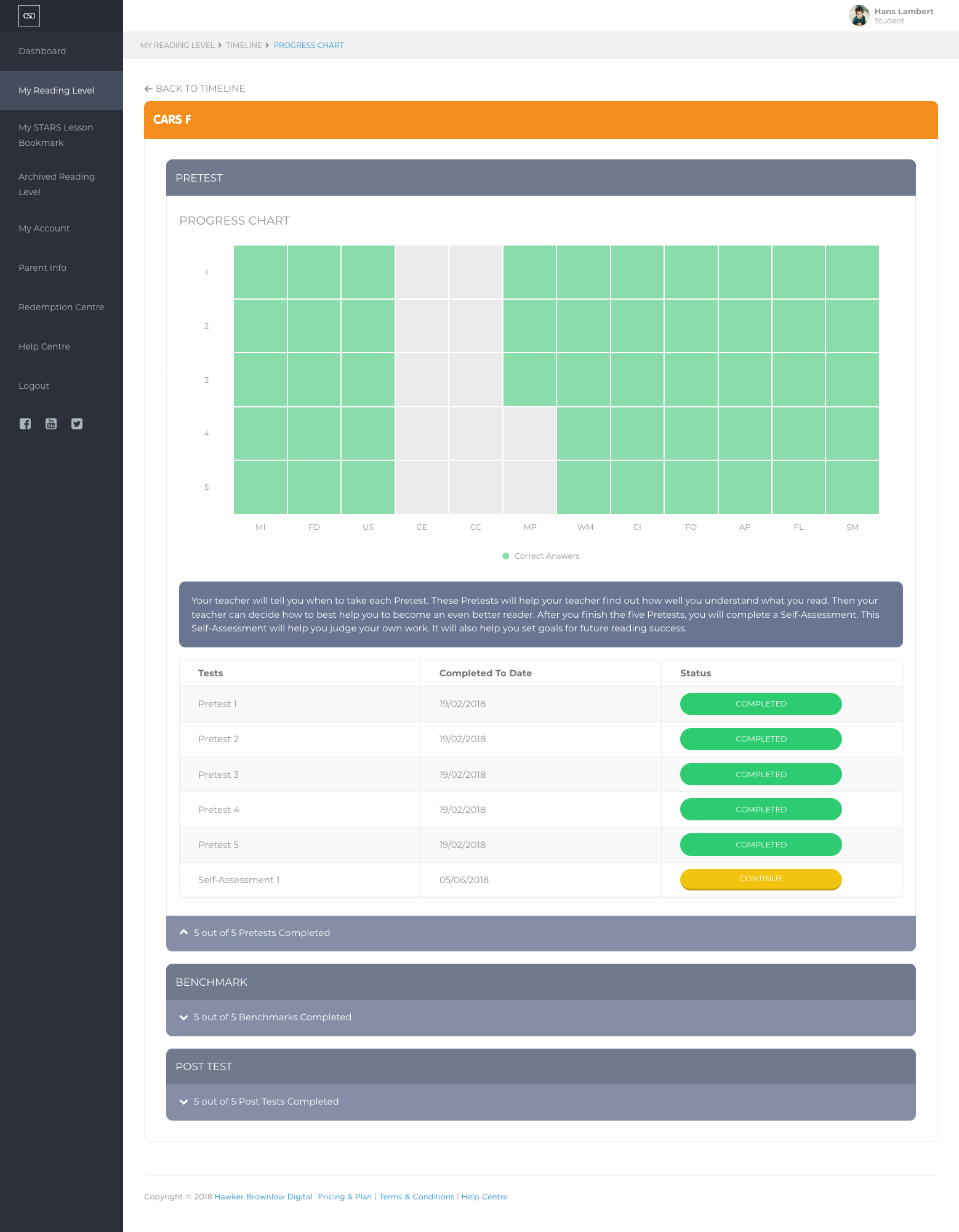
The Progress Chart consists of three sections: Pretest, Benchmark and Post Test, where each section will contain five reading tests; and Self-Assessments, which are only for Pretests and Post Tests. The Self-Assessments are a tool to help the students to review their own performance, and encourage them to set goals for future reading success.

• In each section there is a table that will represent the entire performance for that section. In each table, it will have two sets of labels. The left-hand side label indicates 1 to 5, which represents the test number, e.g. Pretest 1 to 5. The bottom label on the table will represent each strategy that the question covers.
• After each reading test is completed, the student will be able to view their reading test result through the table. For each question that the student has answered correctly it will turn green, otherwise it will remain grey if it is wrong or skipped.
• Each reading test's details will be displayed: Status and Completed to Date. The student can Begin or Continue a test by clicking on its status. Once the status of the test is Completed, the student will not be able to access that reading test.
• Once all five reading tests are completed for each section, the section will collapse as this will let the student focus on the next section.

Please note: For Pretests and Post Tests, the student will be required to complete the Self-Assessments, otherwise the section will not collapse and the assessment will not be marked as COMPLETED.